CBSE Guess > Papers > Important Questions > Class IX > 2011 > Maths > Mathematics By Mr. Amit Kumar Jha

CBSE CLASS IX

Quadrilaterals

Section A

Prove that followings:

1. A diagonal of a parallelogram divides it into two congruent triangles.
2. In a parallelogram, opposite sides and angle are equal.
3. If each pair of opposite sides of quadrilateral is equal, then it is a parallelogram.
4. If in a quadrilateral, each pair of opposite angles is equal, then it is a parallelogram.
5. The diagonals of a parallelogram bisect each other.
6. If the diagonals of a quadrilateral bisect each other, then it is a parallelogram.
7. A quadrilateral is a parallelogram if a pair of opposite sides is equal and parallel.
8. The line drawn through the mid-point of one side of a triangle, parallel to another side bisects the third side.
9. The line segment joining the mid- points of the two sides of a triangle is parallel to the third side.

Section B

1. Show that each angle of a rectangle is a right angle.
2. Show that the diagonal of a rhombus are perpendicular to each other.
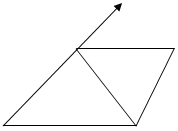
3. ABC is an isosceles triangle in which AB=AC. AD bisects exterior angle PAC and CD||AB. Show that
   (i) angle DAC=angle BCA and
   (ii) ABCD is a parallelogram (||gm).

   

4. Show that the bisectors of the angles of a parallelogram form a rectangle.
5. ABCD is a parallelogram (||gm) in which P and Q are mid-points of opposite side AB and CD. If AQ intersects DP at S and BQ intersects CO at R, show that (i) APCQ is ||gm
   (ii)DPBQ is ||gm
   (iii) PSQR is ||gm

   

6. In Triangle ABC, D, E and Fare respectively the mid points of sides AB, BC and CA. Show that triangle ABC is divided into four congruent triangle by joining D, E and F

   

Section C

1. If the diagonal of a parallelogram are equal, then show that it is a rectangle.
2. Show that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.
3. Show that the diagonals of a square are equal and bisect each other at right angles.
4. Show that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square.
5. In a parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP=BQ. Show that
   
   (ii) AP=CQ
   
   (iv) AQ=CP
   (v) APCQ is a parallelogram.

   

6. In Δ ABC and Δ DEF, AB=DE, AB||DE, BC=EF and BC||EF. Vertices A, B and C are joined to vertices D, E and F respectively. Show that:
   (i) Quadrilateral ABCD is a parallelogram.
   (ii) Quadrilateral BEFC is a parallelogram.
   (iii) AD||CF and AD=CF
   (iv) Quadrilaterals ACFD is a parallelogram
   (v) AC=DF
   (vi) Δ ABC Δ DEF.
7. ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA. AC is a diagonal. Show that:
   (i) SR||AC and SR =1/2 AC
   (ii) PQ=SR
   (iii) PQRS is a parallelogram.
8. ABCD is a rhombus and P, Q, R and S are the mid- point of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
9. ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
10. Show that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
11. ABC is a triangle right angle at C. A line through the mid-points M of hypotenuse AM and parallel to BC intersects AC at D. Show that
    (i) D is the mid –point of AC
    (ii) MD ┴ AC
    (iii) CM=MA=1/2 AB.

 

Submitted By Amit Kumar Jha
Email Id : [email protected]