Q. 18. Using distance formula to show that ,the points with given co-ordinates
(i) FORM AN ISOSCELES TRIANGLE: show that any two sides are equal.
(ii) FORM AN ISOSCELES RIGHT ANGLE TRIANGLE : show that
(a) any two sides are equal
(b)square of one distance is equal to the sum of the squares of other two sides.
(iii) FORM AN EQUILATERAL TRIANGLE : show that all the three sides are equal .
(iv) FORM A RIGHT ANGLED TRIANGLE : show that square of one side is equal to the sum of the squares of the othe two sides.
(v) ARE COLLINEAR : show that one side is equal to the sum of the other two.
(vi) FORM A PARALLELOGRAM : show that opposite sides (i.e., opposite distances)are equal.
(vii) FORM A RECTANGLE : show that (a) opposite sides are equal (b) diagonals are equal
(viii) FORM A RHOMBUS : show that all the four sides (i.e., four distances taken in order )are equal
(ix) FORM A SQUARE : show that (a)four sides are equal (b) diagonals are equal
Q. 19. SECTION FORMULA:
(i) (point of division in between two given points)
Let A( 
,
) and B( 
, 
, ) are two given points. If P(x , y) divides AB internally in the ratio m:n, then
x = 
(ii) co-ordinates of mid-point (ratio is 1:1) of AB are
x =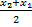
, y= 
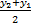i.e( , )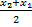
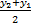Q. 20. CENTROID OF A TRIANGLE: centroid of a triangle is a point where medians meet. It divides each median in the ratio 2:1. Coordinates of centroid of a triangle whose vertices are ( ,), ( , , ) and (x3 ,y3 ) are
(
, 
)
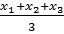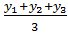Q. 21. AREA OF TRIANGLE: area of triangle with vertices A (x1 ,y1 ) , B ( x2 ,y2 ) and C ( x3 ,y3 ) is given by ar =
ABC .
= 
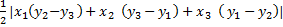
If points A (x1 ,y1 ) , B ( x2 ,y2 ) and C ( x3 ,y3 ) are collinear then area of triangle formed is zero.
Q. 22. On x-axis the point is (x,0)
On y-axis the point is (0,y)
Q. 23. Trigonometry :
sin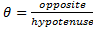
cos 
tan 
cosec
sec 
cot 
