Q. 31. Simplify the rational expression : ![]()
Q. 32. Simplify the rational expression : ![]()
Q. 33. Simplify the rational expression : 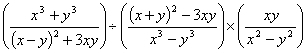
Q. 34. If x = 26/54, y = 28/54, then find the value of 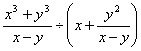
Q. 35. Simplify the rational expression : ![]()
Q. 36. Check whether the equation (x – 3) (x2 + 5) + 3x - 5 = (x2 + 1) (x + 1) – (3x – 7), is quadratic or not, if yes, then solve it.
Q. 37. Solve the equation: pqx2 + (q2 - pr) x = qr.
Q. 38. Find the values of p for which the quadratic equation 2x2 + px + 8 = 0 has real roots.
Q. 39. Solve the equation: (x + 3) / (x + 2) + (x – 3)/ (x – 2) = (2x – 3)/ (x – 1).
Q. 40. Solve the following quadratic equation by using quadratic formula: 9x2 – 6a2x + (a4 – b4) = 0.
Q. 41. Solve the equations:
(i) 4x2 + 12x + 9 = 0.
(ii) 5x2–17x + 35 = 0.
(iii) x2 - 7x - 5 = 0.
Q. 42. Solve the equation: 2 (x – 3)2 + 3 (x – 2) (2x – 3) = 8 (x + 4) (x - 4) – 1.
Q. 43. Solve the following equations: (i) (x + 1)/(x – 1) + (x – 2)/(x + 2) = 3. (ii) (x + 3) / (x – 2) – (1 – x) / x = 17/4.
Q. 44. The sum of the squares of two consecutive positive integers is 545. Find the integers.
Q. 45. Determine two consecutive odd natural numbers, the sum of whose squares is 1154.
Q. 46. The difference of the squares of two numbers is 45. The square of the smaller number is 4 times the larger. Find them.
Q. 47. A fast train takes 2 hours less than a slow train for a journey of 600 km. If the speed of the slow train is 10 km/h less than that of the fast train, find the speeds of the two trains.
Q. 48. A motor-boat, whose speed is 15 km/h in still water, goes 30 km downstream and comes back in a total time of 4 hours and 30 minutes. Find the speed of the stream.
Q. 49. Two trains leave a railway station at the same time. The first train travels due west and the second train due north. The first train travels 5 km/h faster than the second train. If after two hours, they are 50 km apart, find their average speeds.
Q. 50. The sum of the squares of two numbers is 233. If one number is 3 less than twice the other number, find the numbers.
Q. 51. Find the sum of all the multiples of 7 lying between 1 and 100.
Q. 52. Find the total number of terms and hence the sum of the series: 3 + 11 + 19 + ……………………+ 827.
Q. 53. Find the sum of 51 terms of an A.P. whose second and third terms are 14 and 18 respectively.
Q. 54. Find the sum of first 15 terms of an A.P. whose nth term is equal to (9 – 5n).
Q. 55. If five times the 5th term of an A.P. is equal to 8 times the 8th term, then find the sum of its first 25 terms.
Q. 56. The sum of three numbers in A.P. is 12 and the sum of their cubes is 288. Find the three numbers.
Q. 57. Find the sum of all those integers which are multiples of 5 and lie between 84 and 719.
Q. 58. The 5th and 12th terms of an A.P. are 30 and 65 respectively. Find the sum of its first 20 terms.
Q. 59. If the total sum of all the numbers of the series 25, 22, 19,…….., is 116. Find its last term.
Q. 60. An A.P. consists of 60 terms. If the first and the last terms are 7 and 125 respectively, the find its 32nd term.