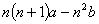Linear Equations in Two Variables
Solve the following equations:
 and
and 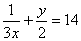
 and
and 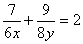
 and
and 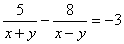
 and
and 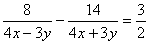
 and
and 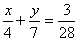
 and
and 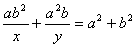
 and
and 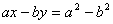
 and
and 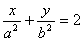
 and
and 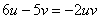
 and
and 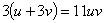
- For what value of k will the system of equations
 and
and  have unique solution?
have unique solution?
- For what value of k will the system of equations
 and
and  have infinite solutions?
have infinite solutions?
- For what value of k will the system of equations
 and
and  have unique solution?
have unique solution?
- For what value of k will the system of equations
 and
and  have no solution?
have no solution?
-
For what value of k will the system of equations  and
and  have no solution?
have no solution?
- For what value of k will the system of equations
 and
and  have infinite solutions?
have infinite solutions?
- A man and a boy can do a piece of work in 15 days which would be done in 2 days by 7 men and 9 boys. How long would it take for one man to complete the work?
- A and B can do piece of work in 16 days, they work together for 4 days, when A leaves, and B alone finished it in 36 days more. In what time can each do the work separately?
- In a triangle ABC ,

 and
and  If
If  Prove that the triangle is right-angled triangle.
Prove that the triangle is right-angled triangle.
- A boat goes 24km upstream and 28km downstream in 6 hours. It goes 30km upstream and 21 km downstream in 6 hours and 30 minutes. Find the speed of the boat in still water and also the speed of the stream.
- Two plugs are opened in the bottom of a cistern containing 192 litres of water, after 3 hours one of them becomes stopped and the cistern is emptied by the other in 11 hours. Had 6 hours elapsed before the stoppage, it would have only required 6 hours more to empty it. How many litres will each plug-hole discharge in one hour, supposing the discharge to be uniform?
- A man wanted to purchase 5 chairs and 5 tables from a market. But for this he had short of Rs.600. He at last purchased 5 chairs and 3 tables with Rs.2005 which he had that time. Find the costs of one chair and one table.
- In a meeting a government officer wanted to distribute certain number of apples equally among the physically handicapped children. If the number of children was 2 less, each of them would have got one apple more. Again when the ten officers present in the day are also included, then each of them will get 3 apples less. Find the number of the handicapped children and the number of apples.
- A farmer wishing to purchase a number of sheep found that if they cost him Rs.42 a head, he would not have money enough by Rs.28, but if they cost him Rs.40 a head, he would then have Rs.40 more than he required, find the number of sheep and the money which he had.
- Says Charles to William, “ If you give me 10 of your marbles, I shall then have justtwice as many as you”, but says William to Charles, “ If you give me 10 of yours, I shall then have three times as many as you”. How many had each?
- The difference of two numbers is 33. When the larger number is divided by the smaller one, the quotient is 2 and the remainder is 4. Find the two numbers.
- A bag contains a total number of 60 coins, Some are of value 50 paise and the others are of 25 paise. If the total amount of money in the bag is Rs.20.50, find the number of coins of each category.
- Some boys hired a bus for a picnic. All paid the same fare. If there had been 4 more boys, each would have had to pay a rupee less and had there been 5 more boys, then each would have paid Rs.2 less. Find the number of boys and the fare each boy paid.
- A man had 10 cows more than his horses. He sold half of the horses and one-third of the cows and still he had left with 10 cows more than his horses. Find the number of cows and the horses he had initially.
- The total cost price of a horse and a cart is Rs.1,200. On selling the horse at a profit of 20% and the cart at a loss of 4%, it found that there was an overall profit of 5%. Find the cost price of the horse.
- Out of 68 students appeared in an examination, 41 passed. If 5 boys pass out of every 8 and 7 girls pass out of every 12, find the numbers of boys and girls appeared in the examination.
- Two places A and B are 70km apart on a road. A man starts by car from A and another man starts from B at the same time. If they travel in the same direction, they meet in seven hours, but if they travel towards each other, they meet in one hour. What are their speeds?
- In 1935, the father's age was four times that of his son. In 1955, the father's age was twice that of his son. Find the year in which the son was born.
- 10 years ago, the age of a man was 35 years more than that of his son. After 5 years the ratio of their ages was 11:4, find their present ages.
- Find the area of the triangle formed by the following pair of lines with the x-axis: x = y and x + y = 2.
- Find the area of the triangle formed by the following pair of lines with the y-axis: 4x + y = 7 and y = 5.
- Draw the graph of he equation 3x - 4y = 12 From the graph find he value of ‘y' if x is -12 and also find the area of the triangle formed by the graph and axes.
Quadratic Equation
Solve for

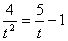
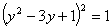
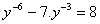
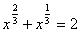
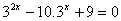
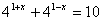
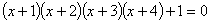
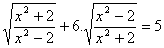
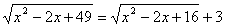
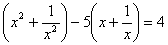
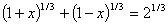
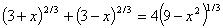
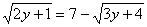
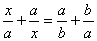
 (solve for x)
(solve for x)
-

- If k is one of the roots of the equation 4x2 + 2x - 1 = 0 then show that the other root is
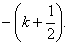
- The sum and the product of the two roots of a quadratic equation are 1 and -12 respectively. Find the equation.
- If the roots of a quadratic equation are 2 and -3 respectively. Find the equation.
- For what values of k will one root of the equation x2 - xx + 8 = 0 be twice the other?
- For what values of m will one root of the equation 2x2 - 14x + m = 0 be in the ratio 3:4?
- For what values of m will the equation x2 - 2(5 + 2m)x + 10m) = 0 has repeated roots.
- If 3 is one of the roots of the equation 2x2 - 7x + k = 0 then find the value of k and the other root.
- If a2 = 5a - 3 and b2 = 5b - 3 find the quadratic equation whose roots are a/b and b/c
- Two examinees solved the equation x2 + px + q = 0 incorrectly. The first one obtained the roots as 8 and 2 by assuming an incorrect value for p, and the second one obtained -9 and -1 by assuming an incorrect vale for q. Find the actual roots of the equation.
- If
 be the roots of the equation x2 + px + q = 0 prove that
be the roots of the equation x2 + px + q = 0 prove that  will be the roots of the equation
will be the roots of the equation 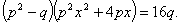
- In a certain class, 1/7 th of the total number of students like football, five times the square root of the total students prefer cricket and the remaining 7 students like hockey. Find the total number of students in the class.
- Divide 16 into two parts such that twice the square of the larger part exceeds the square of the smaller part by 164.
- A swimming pool can be filled by 2 pipes together in 6 hours. If the larger pipe alone takes 5 hours less than the smaller to fill the pool, find the time in which each pipe alone would fill the pool.
- If the perimeter of a rectangular field is 50m and its area is 100 m2. Find the length and breadth.
- A person on tour has Rs.360 for his daily expenses. If he exceeds his tour programme by 4 days he must cut down his daily expenses by Rs.3 per day. Find the number of days of his tour programme.
Arithmetic Progressions
Find the sum:
- 5 + 17 + 29 + 41 ………………… up to the 20 th term.
- 16 + 12 + 8 + 4 …………………..+ (- 60).
-
 to the n th terms.
to the n th terms.
 to the n th terms.]
to the n th terms.]
- Find the sum of the even numbers between 91 and 259.
- Find the sum of the multiples of 11 between 100 and 400.
- The fifth and the ninth terms of an A.P. are 11 and 7 respectively. Find the fourteenth term of the series. Also find the sum of the first sixteen terms.
- Up to what number of terms, will the sum of the series,

be  ?
?
-
If  be the sums of n, 2n and 3n terms of an A.P. then prove that
be the sums of n, 2n and 3n terms of an A.P. then prove that 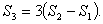
-
The sum of first 9 terms of an A.P. is 171, and of 24 terms is 996. Find the sum of first 41 terms of the A.P.
- In an A.P. the n th term is pand the sum to p terms is q. Show that the first term is

There are four numbers in an A.P. the sum of the two extremes is 8, and product of the means is 15. What are the numbers?
- If the sum of first ‘p' terms of an A.P. is equal to the first ‘q' terms, show that the sum of the first (p + q) terms is zero.
- If a, b, c are in A.P. then show that (b + c), (c + a), (a + b) are also in A.P.
- If (b + c), (c + a), (a + b) are in A.P. then show that


 are also in A.P.
are also in A.P.
- If the sum of the three consecutive terms of an A.P. is 36 and their product is 1140, Find the terms.
- The ratio of three numbers is as 2:5:7. If 7 is subtracted from the second number, then the numbers form an A.P. What were the original numbers?
- If the sum of first n terms of an A.P. is m and that of the first m terms is n, show that the sum of first (m + n) terms is –(m + n).
- Find the 15 th term of an A.P. whose sum up to the first n terms is 3n2 + 7n.
- If a, b, c are respectively pth, qth and rth terms of an A.P. then prove that

Trigonometry
Prove the following identities:
-
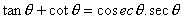
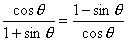
-
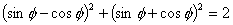
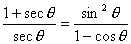


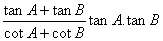

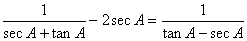












- If
 and
and  show that
show that 
- If
 prove that
prove that 
- If
 prove that
prove that 
- If
 prove that
prove that 
- If
 find the value of
find the value of 
- If
 and
and  show that
show that 
- Evaluate:

- If
 prove that
prove that 
- If


 prove that
prove that 
Answers
1. 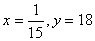 |
2. 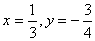 |
3. 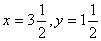 |
4. 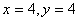 |
5. 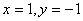 |
6. 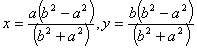 |
| 7. x = a, y = b |
8. 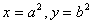 |
9. 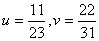 |
10. 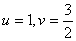 |
11.  |
12. k = 6 |
13. 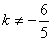 |
14. 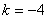 |
15. k = 35/2 |
| 16. k = 3 |
17. 20 days |
18. A in 24 days, B in 48 days |
| 20. 10 km, 4 km |
21. 8 litres, 12 litres |
22. Rs.225, Rs.300 |
| 23. 20, 180 |
24. 34 sheep, Rs.1400 |
25. 22, 26 |
| 26. 29,62 |
27. 22 fifty paise coins, 38 twenty five paise coins |
28. 20 boys, Rs.6 |
| 29. 30 cows, 20 horses |
30. Rs.450 |
31. 32 boys, 36 girls |
| 32. 40km, 30km |
33. In the year 1925 |
34. 60 years, 25 years |
| 35. 1/2 sq. unit |
36. 1/2 sq.unit |
37. 12, 6 sq. units |
38. 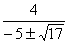 |
39. 1, 4 |
40. 0, 1, 2, 3 |
| 41. 1/2, -1 |
42. 1, -8 |
43. 2, 0 |
44. 1/2, 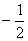 |
45. 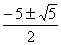 |
46. 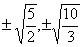 |
| 47. 2, 0 |
48. 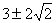 |
49. 1, -1 |
50. 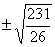 |
51.480, 4 |
52. 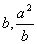 |
53. 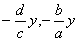 |
54. 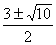 |
56. x2 - x - 12 = 0 |
| 57. x2 + x - 6 |
58. 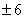 |
59. 24 |
| 60. 2(1/2) |
61. 3(1/2) |
62. 3x2 - 19x + 3 = 0 |
| 63. -2, -8 |
65. 49 |
66. 10, 6 |
| 67. 10 hrs, 15 hrs |
68. 20m, 5m |
69. 20days |
| 70. 2380 |
71. 440 |
72. 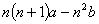 |
73. 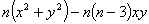 |
74. 14700 |
75. 6831 |
| 76. 2, 120 |
77. 9 |
79. 2747 |
| 81. 1, 3, 5, 7 |
85. 5, 12, 19 or 19, 12, 5 |
86. 28, 70, 98 |
| 88. 94 |
115. 1 |
117. 2 |
 and
and 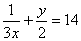
 and
and 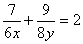
 and
and 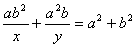
 and
and 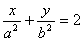
![]() and
and ![]() have no solution?
have no solution?
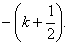
![]() ?
? ![]() be the sums of n, 2n and 3n terms of an A.P. then prove that
be the sums of n, 2n and 3n terms of an A.P. then prove that ![]()
![]()