![]()
CBSE Guess > Papers > Important Questions > Class XII > 2010 > Maths > Mathematics By Mr. M.P.Keshari
Maxima & Minima.
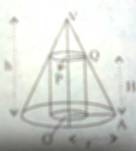
Q.5. Prove that the radius of the right circular cylinder of the greatest curved surface that can be inscribed in a given cone is half of the radius of the cone.
Solution :
Fig
Let height and base radius of the given cone be h and r respectively and let the height and base radius of the inscribed cylinder be H and R respectively.
Now ∆ VPQ ~ ∆ VOA => (h – H)/R = h/r => R = r/h(h – H).
Let S be the curved surface of the cylinder, then
S = 2πRH = 2π(r/h)(h – H)H = (2πr/h) (hH – H2)
Therefore, dS/dH = (2πr/h)(h – 2H) and d2S/dH2 = – 4πr/h.
For maximum and minimum, dS/dH = 0 => H = h/2.
And d2S/dH2]at H = h/2 < 0.
Hence S is maximum.
Now R = r/h(h – H) = r/h(h – h/2) = r/2. [Proved.]
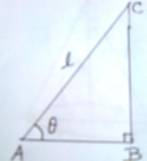
Q.6. A right-angled triangle with constant area S is given. Prove that the hypotenuse of the triangle is least when the triangle is isosceles.
Solution :
Fig
Let length of the hypotenuse be l of the given right-angled triangle ABC at B and LCAB = θ, 0 < θ < π/2.
AB = l cos θ and BC = l sin θ.
Area of Δ ABC = 1/2 (l cos θ)(l sin θ) = S (given).
Or, l2/4 sin 2θ = S
Or, l2 = 4S cosec 2θ
Writing l2 as f(θ) we get, f(θ) = 4S cosec 2θ ---------------- (i)
Differentiating (i) w.r.t. θ we get, f’(θ) = 4S (– cosec 2θ cot 2θ).2
= – 8 S cosec 2θ cot 2θ
and f”(θ) = – 8S{cosec 2 θ (– cosec2 2θ).2 + cot 2θ(– cosec 2θcot 2θ).2}
= 16S cosec 2θ (cosec2 2θ + cot2 2θ).
Now, f’(θ) = 0 => – 8 S cosec 2θ cot 2θ = 0
Or, (1/sin 2θ)(cos 2θ/sin 2θ) = 0
Or, sin 2θ = 0 => 2θ = π/2
Or, θ = π/4.
Also, f”(π/4) = 16 S cosec π/2 (cosec2 π/2 + cot2 π/2)
= 16.1.(1 + 0) = 16 S > 0
Therefore, f(θ) is least when θ = π/4
Or, l is least when θ = π/4.
When θ = π/4, AB = l cos π/4 = l/√2 and BC = l sin π/4 = l/√2.
Hence, the hypotenuse is the least when AB = BC i.e. the triangle is isosceles. [Proved.]
| Maths Paper (With Solutions) By : Mr. M. P. Keshari | ||
| Continuity & Differentiability | Probability | Vector Algebra |
| Differential Equation | Application of Integrals | 3D Geometry |
| Linear Programming | Application of derivatives | Integrals |
| Maxima & Minima | ||
Paper By Mr. M.P.Keshari
Email Id : [email protected]
Ph No. : 09434150289
