![]()
CBSE Guess > Papers > Important Questions > Class XII > 2010 > Maths > Mathematics By Mr. M.P.Keshari
Maxima & Minima.
Q.15. Show that the height of a cylinder of maximum volume that can be inscribed in a cone of height h is 1/3h.
Solution :
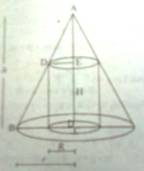
Fig.
Let height of the cylinder be H and base radius be R.
Volume of cylinder V = πR2H ---------------------------------- (1)
ΔABC ~ ΔADE => AC/AE = BC/DE => h/(h – H) = r/R
Therefore, R = r[(h – H)/h] = r[1 – H/h] --------------------------- (2)
Putting R in (1), we get
V = πr2(1 – H/h)2H -------------------------------------- (3)
Differentiating w.r.t.H, we get
dV/dH = πr2[(1 – H/h)2.1 + H.2(1 – H/h)(–1/h)]
= πr2(1 – H/h)[1 – H/h – 2H/h]
dV/dH = πr2(1 – H/h)(1 – 3H/h)
For maximum or minimum, dV/dH = 0
Or, πr2(1 – H/h)(1 – 3H/h) = 0 => H = h, H = h/3.
But H = h is not possible. Hence, H = h/3.
Now, d2V/dH2 = πr2[(1 – H/h)(–3/h) + (1 – 3H/h)(–1/h)]
= (πr2)/h[0 – 3 + 3H/h – 1 + 3H/h]
= (πr2)/h[6H/h – 4]
Therefore, [d2V/dH2]atH=h/3 = πr2/h[6/h.h/3 – 4] = πr2/h(–2) < 0.
Therefore, volume is maximum at H = h/3. [Proved.]
Q.16. Show that the volume of the greatest cylinder that can be inscribed in a cone of height h and semi-vertical α is 4/27 πh3tan2α.
Solution :
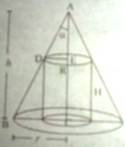
Fig.
Let radius and height of the cylinder be R and H respectively.
Volume of the cylinder V = πR2H ------------------------- (1)
AE = AC – EC = h – H
Therefore, tan α = DE/AE = R/(h – H)
=> R = (h – H)tan α -------------------- (2)
Putting R in (1) we get
V = π(h – H)2 tan2 α.H
Or, V = πtan2 α(h – H)2H --------------------- (3)
Differentiating w.r.t H, we get
dV/dH = πtan2 α[(h – H)2.1 + H.2(h – H)( –1 )]
= πtan2 α(h - H)[h – H – 2H]
= πtan2 α(h – H)(h – 3H) ------------------- (4)
For maxima and minima, dV/dH = 0
Therefore, πtan2 α(h – H)(h – 3H) = 0 => H = h or H = h/3.
As, H = h is not possible, hence, H = h/3.
Now, d2V/dH2 = πtan2 α[(h – H )(– 3) + (h – 3H)(– 1)]
d2V/dH2 = πtan2 α[6H – 4h]
(d2V/dH2)atH=h/3 = πtan2 α(6.h/3 – 4h)
= πtan2α(2h – 4h)
= πtan2 α(– 2h) < 0
Therefore, volume is maximum at H = h/3.
Putting H in (3), we get
Maximum volume = πtan2 α(h – h/3)2.h/3
= πtan2 α.4h2/9.h/3
= 4/27πh2tan2α. [Proved.]
| Maths Paper (With Solutions) By : Mr. M. P. Keshari | ||
| Continuity & Differentiability | Probability | Vector Algebra |
| Differential Equation | Application of Integrals | 3D Geometry |
| Linear Programming | Application of derivatives | Integrals |
| Maxima & Minima | ||
Paper By Mr. M.P.Keshari
Email Id : [email protected]
Ph No. : 09434150289
