![]()
CBSE Guess > Papers > Important Questions > Class XII > 2010 > Maths > Mathematics By Mr. M.P.Keshari
Linear Programming
Q.3. A furniture dealer deals only in two items – tables and chairs. He has Rs10,000 to invest and a space to store at most 60 pieces. A table cost him Rs500 and a chair Rs200. He can sell a table at a profit of Rs50 and a chair at a profit of Rs15. Assume that he can sell all items that he buys. Using linear programming formulate the problem for maximum profit and solve it graphically.
Solution :

Fig.
Let number of tables = x and number of chairs = y. Let P be the profit of the dealer. The required linear programming is :
Maximize : P = 50x + 15y
Subject to constraints
500x + 200y ≤ 10,000 => 5x + 2y ≤ 100; x + y ≤ 60; x ≥ 0, y ≥ 0.
The lines x + y = 60 --------------- (1) and 5x + 2y = 100 --------------- (2) are drawn on the same graph paper.
The shaded region OCD is the feasible region.
Now P = 50x + 15y
At O, P = 0
At C, P = 50×20 = 1,000
At D, P = 15×50 = 750.
Therefore, maximum profit is at C(20, 0). [Ans.]
Q.4. A farmer has a supply of chemical fertilizer of type A which contains 10% of nitrogen and 6% of phosphoric acid and of type B which contains 5% of nitrogen and 10% of phosphoric acid. After soil testing it is found that at least 7 kg of nitrogen and the same quantity of phosphoric acid is required for a good crop. The fertilizer of type A costs Rs5.00 per kg and the type B costs Rs8.00 per kg. Using linear programming find how many kgs of each type of the fertilizer should be bought to meet the requirement and the cost be minimum. Solve the problem graphically.
Solution :
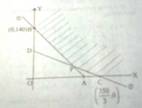
Fig.
Let x kg of type A and y kg of type B fertilizer be mixed by the farmer to meet the requirement with minimum cost. Then linear programming problem is :
Minimize : C = 5x + 8y.
Subject to the constraints
(10/100) x + (5/100) y ≥ 7 ó 2x + y ≥ 140
(6/100) x + (10/100) y ≥ 7 ó 3x + 5y ≥ 350
x ≥ 0, y ≥ 0.
Lines 2x + y = 140 ------------------------------ (1)
and 3x + 5y = 350 ----------------------------- (2)
are drawn on the same graph paper.
The shaded region is thw feasible region. The lines meet at P(50, 40).
Now C = 5x + 8y.
At C(350/3, 0), C = 5×350/3 + 0 = 1750/3 = Rs583.33
At P(50, 40), C = 5×50 + 8×40 = Rs570
At B(0,140), C = 0 + 8 × 140 = Rs1120.
Therefore, cost is minimum at P(50, 40). That is 50 kg of type A and 40 kg of type B is mixed to meet the requirement.
| Maths Paper (With Solutions) By : Mr. M. P. Keshari | ||
| Continuity & Differentiability | Probability | Vector Algebra |
| Differential Equation | Application of Integrals | 3D Geometry |
| Linear Programming | Application of derivatives | Integrals |
| Maxima & Minima | ||
Paper By Mr. M.P.Keshari
Email Id : [email protected]
Ph No. : 09434150289
