![]()
CBSE Guess > Papers > Important Questions > Class XII > 2010 > Maths > Mathematics By Mr. M.P.Keshari
Maxima & Minima.
Q.3. Find the point on the curve y2 = 4x which is nearest to the point (2, –8).
Solution :
Let P(t2, 2t) be the point on y2 = 4x nearest to the point A(2, –8). Then
AP2 = (t2 – 2)2 + (2t + 8)2 = y (say)
Therefore, y = (t2 – 2) + (2t + 8)
= (t4 – 4t2 + 4) + (4t2 + 32t + 64)
= t4 + 32t + 68.
Or, dy/dt = 4t3 + 32 and d2y/dt2 = 12t2.
For maximum and minimum value of y i.e. of AP, dy/dt = 0
Or, 4(t3 + 8) = 0
Or, (t + 2)(t2 – 2t + 4) = 0
Or, t = –2 = 0
As t2 – 2t + 4 = 0 has imaginary values of t.
For, t = – 2, d2y/dt2 = 12 (– 2)2 = 48 > 0
Hence y is minimum => AP is minimum.
Thus the point P(t2, 2t) = P(4, – 4) is the nearest point to the point (2, – 8).
Therefore, the nearest point is (4, – 4) [Ans.]
Q.4. Find the largest possible area of the right-angled triangle whose hypotenuse is 5 cm.
Solution :
.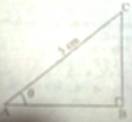
Fig.
Let ABC be a right angled triangle whose hypotenuse AC = 5 cm. Then
AB = 5 cos θ; BC = 5 sin θ
Therefore, A = Area of ∆ABC = 1/2×AB×BC = 25/2.cos θsin θ = 25/4 sin2θ
Therefore, dA/dθ = 25/2.cos 2θ and d2A/dθ2 = – 25 sin2θ
For maximum or minimum dA/dθ = 0
=> cos2θ = 0
=> 2θ = π/2
=> θ = π/4.
d2A/dθ2]at θ = π/4 = – 25 < 0.
Therefore, A is maximum, when θ = π/4.
Largest of the triangle = 25/4 sin π/2
= 25/4 sq. units. [Ans.]
| Maths Paper (With Solutions) By : Mr. M. P. Keshari | ||
| Continuity & Differentiability | Probability | Vector Algebra |
| Differential Equation | Application of Integrals | 3D Geometry |
| Linear Programming | Application of derivatives | Integrals |
| Maxima & Minima | ||
Paper By Mr. M.P.Keshari
Email Id : [email protected]
Ph No. : 09434150289
