![]()
CBSE Guess > Papers > Important Questions > Class XII > 2010 > Maths > Mathematics By Mr. M.P.Keshari
Maxima & Minima.
Q.7. Three sides of a trapezium are equal, each being 10 cm. Find the area of the trapezium when it is maximum.
Solution :
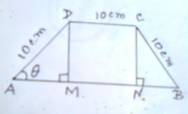
Fig
Let three sides BC, CD and DA of the trapezium ABCD be 10 cm. DM and CN are perpendicular on AB.
ΔAMD ≈ ΔBNC [RHS congruency axiom]
Therefore, AM = NB.
Let LDAM = , 0 < θ < π/2, then AM = 10 cos θ = NB & MD = 10 sin θ = height.
Area of the trapezium, A = 1/2 (AB + DC) × MD = 1/2 (AM + MN + NB + DC) × MD
= 1/2 (10 cos θ + 10 + 10 cos θ + 10 ) ×10 sinθ
= 50 (2 + 2 cos θ) sin θ
= 50 ( 2 sin θ + sin 2θ) ---------------- (i)
Differentiating w.r.t. θ , we get dA/dθ = 50 ( 2 cos θ + 2 cos 2θ . 2)
= 100 (cos θ + cos 2θ) and
d2A/dθ2 = 100 (– sin θ – sin 2θ . 2)
= – 100 (sin θ + 2 sin 2θ).
Now dA/dθ = 0 => 100 ( cos θ + cos 2θ) = 0
Or, cos θ + cos 2θ = 0
Or, 2 cos 3θ/2. cos θ/2 = 0
Either, cos3θ/2 = 0 or cos θ/2 = 0
Either, 3θ/2 = π/2 or θ/2 = π/2 => θ = π/3, π but 0 < θ < π/2.
Hence, θ = π/3.
Also [d2A/dθ2]θ = π/2 = – 100(sinπ/3 + 2sin2π/3) = – 100(√3/2 + 2√3/2) = – 150√3 < 0
Hence, A is maximum when, θ = π/3.
When θ = π/3, A = 50 ( 2.sin π/3 + sin 2π/3) = 50 ( 2.√3/2 + √3/2) = 75√3.
Hence, the maximum area of the trapezium is 75√3. [Ans.]
Q.8. Show that the semi-vertical angle of the right circular cone of given total surface area and maximum volume is sin –11/3.
Solution :

Fig
| Maths Paper (With Solutions) By : Mr. M. P. Keshari | ||
| Continuity & Differentiability | Probability | Vector Algebra |
| Differential Equation | Application of Integrals | 3D Geometry |
| Linear Programming | Application of derivatives | Integrals |
| Maxima & Minima | ||
Paper By Mr. M.P.Keshari
Email Id : [email protected]
Ph No. : 09434150289
