![]()
CBSE Guess > Papers > Important Questions > Class XII > 2010 > Maths > Mathematics By Mr. M.P.Keshari
Maxima & Minima.
Q.21. Three numbers are given whose sum is 180 and the ratio between first two of them is 1:2. if the product of the number is greatest, find the numbers.
Solution :
Let the numbers be x,y and z. And x/y = 1/2 => 2x = y .
Also , x + y + z = 180 => x + 2x + z = 180 => z = 180 – 3x .
Let product of x, y and z be P = xyz = (x)(2x)(180 – 3x)
Or, P = 360 x2 – 6x3
Or, dP/dx = 720 x – 18x2 = 0 [for maxima or minima]
Or, x = 40 .
Againd2P/dx2 = 720 – 36x = 720 – 36 × 40 [at x = 40]
= – 720 < 0 .
Therefore , P is maximum at x = 40 ,
i.e. x = 40 , y = 2x = 2 × 40 = 80 , z = 180 – 3x = 180 – 3 × 40 = 180 – 120 = 60.
Therefore , numbers are 40 , 80 , 60 . [Ans.]
Q.22. ABC is a right-angled triangle of given area S. Find the sides of the triangle for which the area of the circumscribed circle is least.
Solution :
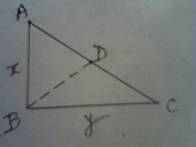
Fig.
Let sides be x and y such that S = 1/2 xy => y = 2S/x -------------- (1)
Circumscribed circle of the triangle ABC will pass through A , B and C. Let D be the centre , then DA = DB = DC .
DA = DC = > D is mid-point of AC , => AD = DC = 1/2 × AC .
Area of circumscribed circle , A = π r2 ,
= π × {1/2 √(x2 + y2)}2. [where r = 1/2 √(x2 + y2)] .
= π/4(x2 + y2)
= π/4 {x2 + (2S/x)2}.
Differentiating w. r. t. x , we get dA/dx = π/4 {2x + 4S2 (– 2/x3)}
= π/4 {2x – 8S2/x3}= 0 [for maxima or minima] Or, 2x4 – 8S2 = 0
Or, x2 = 4S2
Or, S = 1/2 x2
But S = 1/2 xy
Therefore ,1/2 xy = 1/2 x2 => x = y .
Thus area of circumscribed circle is least , when x = y . In other word the right-angled triangle is isosceles triangle and the sides forming right angle are equal. [Ans.]
| Maths Paper (With Solutions) By : Mr. M. P. Keshari | ||
| Continuity & Differentiability | Probability | Vector Algebra |
| Differential Equation | Application of Integrals | 3D Geometry |
| Linear Programming | Application of derivatives | Integrals |
| Maxima & Minima | ||
Paper By Mr. M.P.Keshari
Email Id : mpkeshari@yahoo.com
Ph No. : 09434150289
