![]()
CBSE Guess > Papers > Important Questions > Class XII > 2010 > Maths > Mathematics By Mr. M.P.Keshari
Application of Integrals
8.3. Area Between Two Curve.
Q.1. Using integration, find the area of the region enclosed between two circles x2 + y2 = 1 and (x – 1)2 + y2 = 1.
Solution :
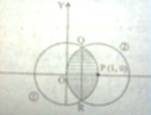
Fig.
The two circles are shown above and the enclosed area is shaded.
The two circles are :
x2 + y2 = 1 ----------- (1) and
(x – 1)2 + y2 = 1 --------------- (2)
These two circles intersect at R(1/2, – √3/2) and Q(1/2, √3/2).
Required area = 2[∫y2 dx + ∫y1dx]
= 2[0∫1/2 y2 dx + 1/2∫1 y1 dx]
= 2[0∫1/2√{1 – (x – 1)2}dx + 1/2∫1√(1 – x2)dx]
= 2[{(x – 1)√(1 – (x – 1)2)/2 + 1/2 sin –1(x – 1)/1}01/2 + {x√(1 – x2)/2 + 1/2 sin –1x}1/21]
= – 1/2√(3/4) + sin –1( –1/2) – 0 – sin –1(–1) + 0 + sin –1(1) – 1/2 √(3/4) – sin –1(1/2)
= (π– π/3) – (√3)/2 = 2π/3 – (√3)/2. sq. units. [Ans.]
Q.2. Using integration, find the area of the region enclosed between the circles x2 + y2 = 4 and (x – 2)2 + y2 = 4.
Solution : – Do yourself. [Ans. = 8π/3 – 2√3]
Q.3. Using integration find the area of the region bounded by the parabola y2 = 4x and the circle 4x2 + 4y2 = 9.
Solution :

Fig.
We have, y2 = 4x ---------------------- (1)
4x2 + 4y2 = 9 ---------------------- (2)
Or, x2 + y2 = 9/4
which is the equation of a circle with centre (0, 0) and radius 3/2.
Solving (1) and (2), we get
4x2 + 4.4x = 9
Or, 4x2 + 18x – 9 = 0
Or, (2x + 9)(2x – 1) = 0 => x = – 9/2, 1/2.
As, x = – 9/2 is negative, it is neglected. Thus x = 1/2.
From (1), y = √(4x) = 2 x1/2 and from (2) y = √(9/4 – x2) = √{(3/2)2 – x2}.
Area of bounded region OADC,
A1 = 2∫ydx = 20∫1/2 2x1/2 dx
= 4[(x3/2)/(3/2)]01/2
= 8/3[(1/2)3/2 – 0]
= (8/3)(1/2)√(1/2)
= 2√2/3.
Area of bounded region ABCD,
A2 = 21/2∫3/2 ydx = 21/2∫3/2√{(3/2)2 – x2}dx
= 2[x/2√{(3/2)2 – x2} + {(3/2)2}/2sin -1{(x/3)/2}]1/23/2
= 2[x/2√(9/4 – x2) + 9/8sin –1(2x/3)]1/23/2
= 2[{0 + 9/8 sin –1(2/3.3/2)} – {(1/2)/2√(9/4 -1/4)
+ sin –1(2/3.1/2}]
= 2[9/8sin -1(1) -1/4√(8/4) – 9/8sin -1(1/3)]
= 2[9/8.π -1/4√2 – 9/8sin -1(1/3)]
= 9/8π – √2/2 – 9/4sin -1(1/3).
Total area = A1 + A2 = 2√2/3 + 9/8π – √2/2 – 9/4sin –1(1/3)
= {4√2 – 3√2}/6 + 9/8π – 9/4sin –1(1/3)
= √2/6 + 9/8π – 9/4sin –1(1/3). [Ans.]
| Maths Paper (With Solutions) By : Mr. M. P. Keshari | ||
| Continuity & Differentiability | Probability | Vector Algebra |
| Differential Equation | Application of Integrals | 3D Geometry |
| Linear Programming | Application of derivatives | Integrals |
| Maxima & Minima | ||
Paper By Mr. M.P.Keshari
Email Id : [email protected]
Ph No. : 09434150289
