Q. 40. Find a quadratic polynomial whose sum and product of the zeros are 
and 
respectively.
Q. 41. If each side of an equilateral triangle is ‘2a’ units, what is the length of its altitude?(√3a)
Q. 42. A solid cylinder of radius ‘r’ cm and height ‘h’ cm is melted and changed into a right circular cone of radius ‘4r; cm. Find the height of the cone. (h=3/16)
Q. 43. Find the value of ‘k’ for which the quadratic equation (k+1) x2 + (k+4) x + 1 = 0 has equal Roots.(2,-6)
Q. 44. Find the value of p for which the points (-1, 3), (2, p) and (5, -1) are collinear.(-3)
Q. 45. If the point P(x, y) is equidistant from the points A (5,1) and B(-1, 5), prove that 3x = 2y.
Q. 46.How many terms of the AP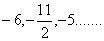
will give the sum zero.(-5,5)
Q. 47. Prove that the intercept of a tangent between two parallel tangents to a circle subtends a right angle at the centre.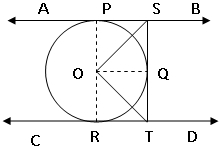
Q. 48. If the sum of first n terms of an A.P. is given by Sn = 4n2 – 3n, find the nth term of the A.P.
Q. 49. Obtain all the zeroes of the polynomial 3x4 + 6x3 - 2x3 – 10x + 5, if two of its zeroes are √5 / √3 and -√5 / √3.
Q. 50. One letter is selected at random from the word ‘UNNECESSARY’. Find the probability of selecting an E. (2/11)
Q. 51. Three cubes each of sides 5 cm are joined end to end .Find the surface area of the resulting solid. 250
Q. 52. The lengths of two cylinders are in the ratio 3:1 and their diameters are in the ratio 1:2 .Calculate the ratio of their volumes.(3:4)
Q. 53. Tickets numbered from 1 to 20 are mixed up together and then a ticket is drawn at random. What is the probability that the ticket has a number which is a number of 3 or 7?(2/5)
Q. 54. Find the least number of coins of diameter 2.5 cm and height 3 mm which are to be melted to form a solid cylinder of radius 3 cm and height 5 cm.(96)
Q. 55. The radii of two cylinders are in the ratio 2:3 and their heights are in 5:3. Calculate the ratio of their volume.(20/81)
Q. 56. The volume of two spheres are in the ratio 64 : 27. Find their radii if the sum of their radii is 21cm.the height of a cylinder is 15 cm. the curved surface area is 660 cm². find the radius .(7 cm)
Q. 57. The circumference of the edge f a hemispherical bowl is 132 cm. find the capacity of the bowl.(19404 cm3)
Q. 58. An electric pole is 10 m high. If its shadow is 10√3 m in length. Find the elevation of the sun.(30)
Q. 59. The largest cube is carved out of a cube of radius 7 cm. find the volume of the sphere.(1437.3 cm3)
Q. 60. A vessel is in the form of a hemispherical bowl mounted by a hollow cylinder. The diameter of the hemisphere is 14 cm and the total height of the vessel is 13 cm. Find the capacity of the vessel.(27020.6cm3)
