Q. 61. Prove that the ratio of the areas of similar triangles is equal to the ratio of the squares on the corresponding sides.Using the above result, prove that “ if the areas of two similar triangles are equal , they are congruent”.
Q. 62. If a line is drawn parallel to one side of a triangle, prove that the other two sides are divided in the same ratio. Using the above result, find AB when in ∆ABC , DE ║ BC so that AD = 2.4 cm , AE = 3.2 cm and EC = 4.8 cm.(6 cm)
Q. 63. In a triangle, if square of one side is equal to the sum of the squares of other two sides, then angle opposite the first side is a right angle.using the converse of above theorem determines the length of an altitude of an equilateral triangle of side 2a.(√3a)
Q. 64. The ratio of areas of similar triangles is equal to the ratio of the squares on the corresponding sides. Prove.Using the above theorem, prove that the area of the equilateral triangle described on the side of a square is half the area of the equilateral triangle described on the diagonal.
Q. 65. If the radii of the ends of a bucket 45cm high are 28cm and 7cm.Find its capacity and surface area.(48510 cm3 , 5461.5 cm2)
Q. 66. A bucket is in the form of a frustum of a cone and holes 28.490 litres of water. The radii of the top and bottom are 28cm and 21cm respectively. Find the height of the bucket.(15 cm)
Q. 67. A spherical cannon ball, 28cm in diameter is melted and cast into a right circular conical mould, the base of which is 35cm in diameter. Find the height of the cone.(40)
Q. 68. A toy is in the form of a cone mounted on a hemisphere of radius 7cm. The total height of the toy is 9.5cm. Find the total surface area and the volume of the toy. (470.8 , 847cm3)
Q. 69. A spherical shell of lead, whose external diameter is 18cm, is melted and recast into a right circular cylinder, whose height is 8cm and diameter 12cm. Determine the internal diameter of the shell. (4 cm)
Q. 70. A metallic right circular cone 20cm height and whose vertical angle are 60° is cut into two part at the middle of its height by a plane parallel to its base. if the frustum so obtained is drawn into a wire of diameter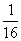 
cm, find the length of the wire.(7964.4 m3)
Q. 71. Water in a canal, 30 dm wide and 12 dm deep is flowing with a velocity of 10 km/h. How much area will it irrigate in 30 minutes, if 4 cm of standing water is required for irrigation?(450000m3)
Q. 72. A solid iron pole consists of cylinder of height 220cm and base diameter 24cm, which is surmounted by another cylinder of height 60cm and radius 8cm. find the mass of the pole, given that 1cm3 of iron has approximately 8g mass. (Use p=3.14).(892.26)
Q. 73. The height of a cone is 30 cm. A small cone is cut off at the top by a plane parallel to the base. If its volume be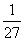 
of the volume of the given cone, at what height above the base, the section has been made? (20)
Q. 74. If the nth terms of an A.P is (2n + 1), find the sum of first n terms of the A.P.
Q. 75. Find the sum of first 10 terms of an A.P., in which 3rd term is 7 and 7th term is two more than thrice of its 3rd term.
Q. 76. If the sum of n terms of an A.P.is same as the sum of its n terms, show that the sum of its (m + n) terms is zero.
Q. 77. Find the sum of first n odd natural numbers.
Q. 78. If the 8th terms of an A.P.is 31 and the 15th terms is 16 more than the 11th terms find the sum of first 20 terms.
Q. 79. How many terms of A.P.: 24,21,18,…….. Must be taken so that their sum is 78?
Q. 80. The angles of a triangle are in AP.If the greatest angle equals the sum of the other two, find the angles.
Q. 81. How many terms of the sequence 18,16,14…… should be taken so that their sum is zero.
