CBSE Guess > Papers > Question Papers > Class X > 2009 > Mathematics > Mathematics
SECTION C
Questions number 16 to 25 carry 3 marks each.
Q. 16. Prove that  is an irrational number.
is an irrational number.
Sol. See Q. 16, 2009 (II Delhi). [Page 325 / 2007.
Q. 17. Find all other zeroes of x4 + x3– 23x2 – 3x + 60, if it is given that two of its zeroes are and –
and –  .
.
Sol. Since two zeroes are  and – .
and – . (x –
(x –  ) (x +
) (x +  ) = x2 – 3 is a factor of given polynomial.
) = x2 – 3 is a factor of given polynomial.
 x4 + x3–23x2– 3x + 60
x4 + x3–23x2– 3x + 60
= (x2 – 3) (x2 + x – 20)
= (x2 – 3) (x2 + 5x – 4x – 20)
= (x2 – 3) [x(x + 5) – 4(x + 5)]
= (x + 3 )(x – 3 )(x – 4)(x + 5)
All other zeroes are x – 4 = 0 or x + 5 = 0
x = 4 or x = – 5
Q. 18. Check graphically whether the pair of equations 3x – 2y + 2 = 0 and  x – y + 3 = 0, is consistent. Also find the coordinates of the points where the graphs of the equations meet the y-axis.
x – y + 3 = 0, is consistent. Also find the coordinates of the points where the graphs of the equations meet the y-axis.
Sol. 3x – 2y + 2 = 0  x – y + 3 = 0
x – y + 3 = 0
 3x + 2 = 2y
3x + 2 = 2y  x + 3 = y
x + 3 = y

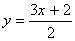
| x | 0 | 2 | -2 |
| y | 1 | 4 | -2 |
| x | 0 | 2 | -2 |
| y | 3 | 6 | 0 |
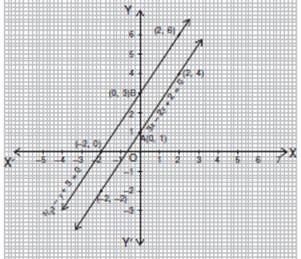
By plotting the points and joining them, the lines donot intersect anywhere, i.e., they are parallel.
 Given pair of equations is not consistent, i.e., inconsistent.
Given pair of equations is not consistent, i.e., inconsistent.
 The equation 3x – 2y + 2 = 0 meets the y-axis at A(0, 1)
The equation 3x – 2y + 2 = 0 meets the y-axis at A(0, 1)
The equation  x – y + 3 = 0 meets the y-axis at B(0, 3).
x – y + 3 = 0 meets the y-axis at B(0, 3).
| Mathematics 2009 Question Papers Class X | |||||||||
| Delhi | Outside Delhi | Compartment Delhi | Outside Delhi | Foreign | |||||
| Set 1 (PDF) | Set 1 (PDF) | Set 1 | Set 1 | Set 1 (PDF) | |||||
| Set 2 | Set 2 | ||||||||
| Set 3 | Set 3 | ||||||||