Height and Distance
Some times we are required to find the height of a tower, tree, building and distance of a ship from light house, width of a river etc. We cannot measure them accurately, though we can find them using the knowledge of trigonometric ratio.
Line of sight: -
When we see an object standing on the ground. The line of sight is the line from our eye to the object, we see.
Angle of Elevation:-
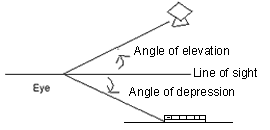
When the object is above the horizontal level of our eye, we have to turn our head upwards to see an object. In this process, our eyes move through an angle which is called angle of elevation.
Angle of Depression:-
When the object is on the ground and the observer is on a building then the object is below the level of the eye of the observer. The observer has to turn his head downward to see the object. In doing so, his eyes move through an angle which is called angle of depression.
Example 1. A man is standing on the deck of a ship, which is 8m above water level. He observes the angle of elevation of the top of a hill as 600 and angle of depression of the base of the hill as 300. Calculate the distance of the hill from the ship and the height of the hill.
Solution: - Let B be man, D the base of the hill, x be the distance of hill from the ship and h + 8 be the height of the hill.
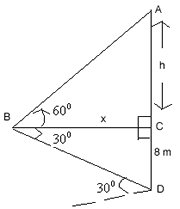
In
tan 600 = AC/BC
In
tan 300 = CD/BC
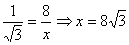
Height of the hill = h + 8 = 24 + 8 = 32m
Distance of the hill from the ship =
| Subjects | Maths (Part-1) by Mr. M. P. Keshari |
| Chapter 9 | Circle |
| Chapter 10 | Tangents to a circle |
| Chapter 11 | Geometrical Construction |
| Chapter 12 | Troigonometry |
| Chapter 13 | Height and Distance |
| Chapter 14 | Mensuration |
| Chapter 15 | Statistics |
| Chapter 16 | Probability |
| Chapter 17 | Co-ordinate Geometry |