Sometimes we say, “probably it may rain” or “Probably he may get more than 90% in the examination" etc. These are elements of certainty. Means we are not certain about some things. In mathematics these comes under Probability.
The theory of probability is widely used in the area of natural as well as social science.
Probability as a Measure of Uncertainty
Suppose we through a die which is a well balanced cube with its six faces marked numbers from 1 to 6, one number of one face, we see the number which come up on its uppermost face. A die can fall with any of its face upper most.
The number on each of the face is equally libely and possible outcome. There are six equally likely ealy outcomes: 1, 2, 3, 4, 5 or 6 in a single throw of a die. The chance of any number ‘say 3’ to come up is 1 out of 6. That is probability of 3 coming up is 1/6
i.e. p(3) = 1/6
Similarly in tossing a coin, we may get either head (H) or tail (T) up and P(H) = ½
Hence probability of an event E is
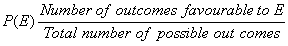
There are only six possible outcome in a single throw of a die. If we want to find probability of 7 or 8 to come up, then in that case number of possible or favorable outcome is O (zero), hence P(7) = 0/6 = 0
i.e. probability of an impossible event is zero.
If we consider to find the probability of number less than 7, then all six cases are favorable and hence P(number less than 7) = 6/6 = 1
i.e. probability of sure event is 1
Now, P (3) = 1/6, then probability of numbers of other than 3 must be 5/6
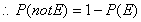
Example 1. An unbiased dice is tossed.
Solution:-
n(s) = 6
E = event of getting a number greater than 4
= {5, 6}
n (E) = 2
P (> 4) = Probability of a number greater than 4
= n(E)/n(S) = 2/6 = 1/3
n (E) = 3
P(Prime number) = Probability of a prime number
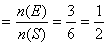
| Subjects | Maths (Part-1) by Mr. M. P. Keshari |
| Chapter 9 | Circle |
| Chapter 10 | Tangents to a circle |
| Chapter 11 | Geometrical Construction |
| Chapter 12 | Troigonometry |
| Chapter 13 | Height and Distance |
| Chapter 14 | Mensuration |
| Chapter 15 | Statistics |
| Chapter 16 | Probability |
| Chapter 17 | Co-ordinate Geometry |