We are already familiar with plotting a point on a plane graph paper. For this we take two perpendicular lines XoX’ and YoY’ intersecting at O. XOX’ is called x-axis or abscissa and YoY’ is called y-axis or ordinate.
Point in a plane
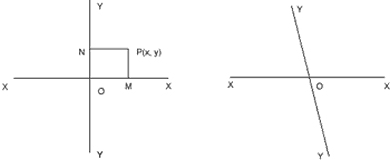
Let us take a point P in a plane. Let XOX’ and YOY’ be pendicualr to each other at O. 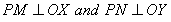 are drawn. If OM = x and ON = y then x-coordinate of P is x and y-coordinate of P is y. Here we write x-coordinate first. Hence (x, y) and (y, x) are different point whenever
are drawn. If OM = x and ON = y then x-coordinate of P is x and y-coordinate of P is y. Here we write x-coordinate first. Hence (x, y) and (y, x) are different point whenever 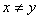 .
.
The two lines XOX’ and YOY’ divides the plane into four parts called quadrants. XOY, YOX’, X’OY’ and Y’OX are respectively the first second, third and and fourth quadrants. We take the direction from O to X and O to Y as positive and the direction from O to X’ and O to Y’ as negative.
Distance between two points
Let P (x1, y1) and Q (x2, y2) be the two points. We have to find PQ.
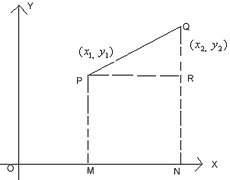
OM = x1, PM = y1 = RN
ON = x2, QN = y2
PR = MN = ON – OM
= x2 – x1
QR = QN – RN = y2 – y1
By Pythagoras theorem
PQ2 = PR2 + QR2
= (x2 - x1)2 + (y2 – y1)2
If x1 = 0, y1 = 0, x2 = x and y2 = y
Then
Section Formula
Let P (x, y) divided a line AB such that AP : PB = m1 : m2.
Let coordinates of A are (x1, y1) and B are (x2, y2).
It is obvious that
Taking,
Similarity
Note
(i) if P is mid point of AB, then AP : PB = 1 : 1
(ii) If m1 : m2 = k, then coordinates of P are
| Subjects | Maths (Part-1) by Mr. M. P. Keshari |
| Chapter 9 | Circle |
| Chapter 10 | Tangents to a circle |
| Chapter 11 | Geometrical Construction |
| Chapter 12 | Troigonometry |
| Chapter 13 | Height and Distance |
| Chapter 14 | Mensuration |
| Chapter 15 | Statistics |
| Chapter 16 | Probability |
| Chapter 17 | Co-ordinate Geometry |