Chapter 9 : Circle

• Circle is a closed figure of points which are at a constant distance from a fixed points, centre and constant distance is called radius.
• Two circles are congruent if and only if they have equal radii.
• Equal chords of a circle subtend equal angles at the centre and conversely.
• Two arcs of a circle are congruent if their corresponding chords are equal and conversely.
• The perpendicular drawn from the centre of a circle to a chord bisects the chord.
• The line drawn through the centre of a circle to bisect a chord is perpendicular to the chord.

Theorem 1. There is one and only one circle passing through three non-collinear points.

Given:- A, B and C are three non-collinear points

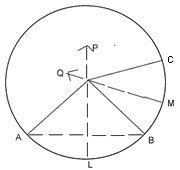
To prove:- One and only one circle are drawn through the points A, B and C.

Construction:- AB and BC are joined PL and QM are drawn perpendicular bisectors respectively of AB and BC to intersect at O.
OA, OB and OC are joined.

Proof:- O lie on PL, the perpendicular bisector of AB

OA = OB ........................(i)

similarty OB = OC...........................(ii)

from (i) and (ii)

OA = OB = OC = r, say

A circle is drawn taking O as centre and r as radius to pass through A, B and C.

Let there be another centre O’ and another radius s, of circle through A, B and C. O’ must lie on PL and QM. As two lines can intersect at only one point. Hence O and O’ coincide.

OA = O' A = r = s

Hence there is unique circle passing through A, B and C.